Chapter I. Introduction and Literature Review
Sheet metal forming processes are among the most important metal-working operations. These processes account for a sizable proportion of the manufactured goods made in industrialized countries each year. Furthermore, to reduce the cost and increase the performance of the manufactured products, in addition to the environmental concern, more and more light weight and high strength materials have been used as a substitute to the conventional steel. These materials usually have limited formability, thus, a thorough understanding of the deformation processes and the factors limiting the forming of sound parts is important, not only from a scientific or engineering viewpoint, but also from an economic viewpoint.
In sheet metal forming operations, the amount of useful deformation is limited by the occurrence of unstable deformation which mainly takes the form of localized necking or wrinkling. Failure by wrinkling occurs when the dominant stresses are compressive, tending to cause thickening of the material. Localized necking occurs when the stress state leads to an increase in the surface area of the sheet at the cost of a reduction in the thickness.
There are two kinds of neck, i.e., the diffuse neck (so called because its extension is much greater than the sheet thickness), and the localized necking (through thickness thinning), which is terminated by final separation or fracture. After the localized neck initiates, further deformation of the material concentrates in this localized region, and the deformation in the homogeneous region vanishes completely. So the localized neck is a very important phenomenon in determining the amount of useful deformation that can be imposed on a workpiece. The mechanism for the initiation of the localized band is very complicated, roughly speaking, this phenomenon can be attributed to the softening effect, for example, the geometric softening (i.e, the decrease with strain of the cross-section area which bears the forming load, the generation of voids), or material softening (flow stress decreases with the increase of the effective strain).
The studies conducted on the analysis of sheet metal formability are too broad to be reviewed exhaustively, the objective of this chapter is to review pertinent theoretical studies related to the analysis of forming limit diagrams (FLDs), and the theories advanced toward the understanding and predicting such strains under complex loading conditions will be described. Of particular interest are the M-K method and linear perturbation analysis.
In many sheet-metal forming operations, the deformation is predominately stretching. When a sheet is progressively thinned, two modes of plastic instability are possible, i.e. diffuse and localized necking (Figure 1).
As early as 1963, a study of failure in biaxially stretched sheets by Keeler and Backofen [1963] showed the existence of what is known as forming limit diagrams (FLDs). The main discovery was that the largest principal strain before any localized thinning in a sheet increased as the degree of biaxiality increased. They had tested several materials including steel, copper, brass and aluminum sheets by stretching them over solid punches. Later, Keeler [1965] found the material properties have great effect on the strain distribution in biaxial stretching of sheet metal. He pointed out that when the material work-hardening exponent, n, is higher, the strain distribution will be relatively homogeneous. On the contrary, materials having lower n values develop sharp strain gradients and the deformation (strain) concentrates in a very small region, then causing premature failure. He constructed a map in principal strain space (e1, e2) which separated safe strain states that a material could provide from the more severe states which would lead to failure. By definition, e1 is the major principal strain, and e2 is the minor principal strain. In other words, FLDs show the combination of major and minor in-plane principal strains beyond which failure occurs.With further development of the experimental techniques by Goodwin [1968], a FLD for mild steel was obtained which served as a criterion for most stamping processes. Because of the contribution of Keeler and Goodwin to the understanding of material formability, the developed FLDs for carbon-steel stamping are often referred to as Keeler-Goodwin diagrams. The FLDs cover strain states from uniaxial tension through plane strain to balanced biaxial tension.
Experimental methods have been widely applied to solve production problems in the sheet metal industry [Hecker, 1973a,b; 1975a, b; 1976]. However, in order to better understand material forming limit diagrams and effectively apply the theoretical predictions to the actual design of sheet metal forming processes, there have been intense researches in developing theoretical FLDs.
Forming limits of sheet metals are influenced by several physical factors of which the most important ones are material work-hardening, strain rate sensitivity, plastic anisotropy, the development of structural damage, in-plane and out-of-plane deformation, and strain path. A bewildering number of different theoretical approaches have been proposed to explain the localized necks in biaxial tensile fields. Up to now, there have been two broad theoretical frameworks to explain necking in biaxial tensile fields. i.e.
1. M-K method. The assumptions of an initial weakness, imperfection or inhomogeneity in the sheet; as straining proceeds, the imperfection gradually develops into a neck [Marciniak and Kuczynski, 1965]. This method is a non-linear method.
2. Linear method. It describes the initiation of localized band of straining in an otherwise uniform sheet, in order to obtain an explicit expression for predicting the limit strains.[Hill, 1952, Storen and Rice, 1975; etc.].
In the following, we will review the pertinent studies of FLDs using these two methods.
To predict the limit strains in sheet metals stretched under conditions such that the surface strains were everywhere positive, Marciniak and Kuczynski [1967] introduced imperfections into sheets to allow necking to take place. They assumed an inhomogeneity in the form of a shallow groove perpendicular to the axial of maximum principal stress, as shown in figure 1.2. This initial inhomogeneity grows continuously with plastic straining to form eventually a localized neck. We call the groove region B and the area outside the groove A, and subject the region A to an uniform proportional straining.
It is further assumed that the groove strain component in the band direction is always the same as the corresponding strain outside the groove during straining. Although the strain ratio (the ratio of minor strain over major strain) outside the groove remains constant during straining, it decreases inside the groove. Eventually the deformation in the groove approaches plane strain deformation (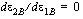
). At this stage, the principal strains outside the groove are identified as the limit strains for this material under the corresponding deformation.
Practically, this type of inhomogeneity could be a local thickness variation, which may originate from surface roughness or prior processing. This problem has been simplified to a one-dimensional one when the imperfection is a geometrical thickness variation or a material property variation that is a function of only the coordinate perpendicular to the infinitely long band. Because of the plane stress assumption, the stress and strain increments inside the neck can be solved directly in terms of the strain increments prescribed outside the band. The plastic properties of the sheet materials were based on the model of anisotropy put forward by Hill [1950]. In this analysis, they only covered the region where both principal strain components were positive. However, this idea led to major developments in the prediction of both regions of the FLDs, and this method is called M-K method.
Azrin and Backofen [1970] subjected a large number of materials to in-plane stretching, they discovered that fractional ratios f0 (=tA/tB) of about 0.97 or less were required to obtain agreement between the Marciniak analysis and the experiments. Grooves of this order of magnitude should be recognizable with the bare eye - which they were not. Accordingly, even though the M-K method may be very easy to understand, there is an inconsistency between the predictions and the experimental data. Similar trends have also been observed by Sower and Duncan [1971] and Marciniak et al. [1973]. In addition, Sower and Duncan also found that the M-K method predicted a large dependence of the limit strains on the value of R.
Ghosh [1973] found that the material strain rate sensitivity becomes important after the maximum of the axial stress vs axial strain curve has been reached. The additional hardening effect due to the strain rate sensitivity plays a significant role in increasing the forming limits by preventing a too rapid concentration of the strains inside the neck.
M-K method tends to give very high limit strain when the strain ratios near balanced biaxial tension. In other words, the M-K method underpredictes the limit strains near plane strain deformation, but overpredictes them in the equibiaxial stretching regime.
The effects of different types of initial nonuniformity on FLDs have been examined by several authors [Van Minh, et al. 1975; Yamaguchi and Mellor, 1976]. Tadros and Mellor [1975] proposed that the localized neck is initiated not at the beginning of stretching but at the Swift instability. They also carried out an experiment [Tadros and Mellor, 1978] which showed that there was no significant necking process up to the Swift instability.
Even though their theory was initially applied only to the region where both strain components are positive, their theory led to major developments in the prediction of FLDs. Further detailed analyses based on the concept of an initial nonuniformity were carried out by Hutchinson and Neale [1978] where the entire FLD was predicted. Their work has made important contributions to gaining insight into the roles of constitutive equations and plasticity theories on FLDs.
Since the pioneering work by these afore mentioned authors, the M-K method has been adopted by other researchers. The sources of disagreement between the calculated and observed FLDs have been identified and studied in detail, resulting in refined models, and reasonable quantitative correlation has been obtained between analytical and experimental limit strains. The effects which influence the FLD will be reviewed in the remainder of this section.
1. 3. 1 The effect of material hardening
It is well known that the rate of work hardening plays an important role in the formability of sheet metals, and the strain-hardening exponent n and the strain rate-hardening exponent m have long been used as an important measure of (stretching) formability. In the original M-K model [Marciniak and Kuczynski, 1967], an empirical strain hardening law was adopted, i.e.
where 
denotes the effective stress, 
are the prestrain and the effective strain respectively, n is the strain hardening exponent, and k is the strength constant.
Laukonis and Ghosh [Laukonis and Ghosh 1978] carried out in-plane deformation studies of an AK steel and an aluminum alloy. They found that strain rate effect is very important to AK steel, especially for the deformation mode near biaxial stretching, while aluminum is insensitive to strain rate. The importance of even a small positive strain-rate sensitivity was explained by Marciniak, Kuczynski, and Pokora [1973]. They used a simplified relation for the flow stress and strain & strain rate:
where 
denotes the effective strain rate and m is the strain-rate sensitivity exponent. Calculations considering the rate effect have brought closer agreement with experiment [Ghosh and Hecker, 1975]. It is found that even a small m can drastically improve the material formability [Ghosh, 1977; Hutchinson and Neale, 1978a; Barata da Rocha, 1989; and Zhao et al, 1996]. Neale and Chater [1980] and Lee and Zaverl [1982] examined the combined effects of material strain-rate sensitivity and anisotropy on sheet necking. Strain rate sensitivity was also seen to alter the shapes of forming limit curves. Material strain-rate dependence is seen to have a substantial effect.
Kinematic hardening - In the above analysis, the material work-hardening effect was assumed to be isotropic, i.e., the yield surface retains the same shape and the same origin during hardening, with only the size of the yield surface changing. This involves an isotropic expansion of the yield surface. In problems of plastic stability, this may be an unfortunate assumption since work hardening causes the yield surface curvature to grow become unrealistically large, which greatly stabilizes plastic flow and leads to unrealistic predictions of the onset of the instability. It is well known that other models with anisotropic hardening give a better description of phenomenon, e.g., the Bauschinger effect.
One of the simplest anisotropic hardening rules is kinematic hardening. In kinematic hardening, the size and shape of the yield surface remain constant, but the origin of this surface translates according to the current stress state. The basic kinematic hardening rule also requires only a single parameter, i.e. the current origin of the yield surface. Kinematic hardening is mainly of interest in cases where the Bauschinger effect is important.
Tvergaard [1978] studied sheet metal necking using a kinematic hardening model. This model was found to accelerate strain localization in the same way as the corner models, although to a lower extent. Tvergaard pointed out that the kinematic hardening model could be interpreted as a model of a material with an expanding, smooth yield surface that develops a rounded vertex at the loading point with a local curvature equal to that of the initial yield surface. He found that the forming limit curves predicted by kinematic hardening are in far better agreement with experimental results than the similar curves predicted by standard flow theory with isotropic hardening. Kinematic hardening may give a reasonable description of the actual material behavior. This effect of kinematic hardening is particularly strong for a high strength material, for which a considerable translation of the yield surface occurs in stress space.
Using the M-K method to compare the effect of isotropic hardening and of the Prager-Ziegler kinematic hardening on the FLDs, Lu and Lee [1987] also found that the kinematic hardening model predicted forming limits that were closer to experimental data for AK steel sheets under proportional loading. On the other hand, the isotropic hardening model gives better predictions of the forming limits with uniaxial prestrain followed by equibiaxial straining. The overall shapes of the limit strains predicted by both isotropic and kinematic models are similar for most loading histories. However, the kinematic model can predict the lower forming limits under subsequent loading with positive strain ratios.
Strain Gradient - To analyze the deformation thoughoutly, the constitutive relation for effective or flow stress should be given to represent the material mechanical properties, which can account for both the homogeneous and nonhomogeneous deformation. A power law hardening rule is commonly used to describe material behavior in sheet metal applications. However, this or other similar relations do not distinguish between the different material properties and behavior inside and outside the neck. In conventional methods, the stress-strain relation is obtained in homogeneous deformation. There is no strain gradient effect in this deformation, so the flow stress is only related to the local effective strain and/or strain rate. To account for the strain gradient effect corresponding to the initiation of the strain localization, a gradient -dependent flow stress has been proposed [Aifantis, 1984].
Based on Aifantis's strain gradient theory [Aifantis 1984], Wang et al. [1995 and1996] incorporated the strain gradient theory into the M-K method to analyze the deformation localization, and to predict the corresponding FLDs. The higher order strain gradient (second order strain gradient) was used in the power law hardening equation to describe the different material properties inside and outside the localized region. According to the studies of Zbib and Aifantis [1988], it is seen that the orientation of the localized band is insensitive to the strain gradients. Wang et al [1996] followed Hill's criterion [1952] and simplified this problem by assuming that the localized necking initiates along the zero extension direction for the left hand side of the FLD. The localized band was assumed to initiate along the minor strain direction for positive strain ratios as proposed by Marciniak and Kuczynski [1967]. This approach introduces an internal length scale into the constitutive equations and takes into account the effects of deformation inhomogeneity. It overcomes the imperfection sensitivity encountered in the conventional M-K method. Shi and Gerdeen [1991] used Barlat and Lian's nonquadratic anisotropic yield criterion [Barlat and Lian, 1989] and strain gradient theory in the constitutive equation to account for the effect of the curvature of the punch on localized necking in anisotropic sheets. The effect of the strain gradient resulting from deforming a flat sheet into a curved sheet is considered in the prediction of FLDs based on the M-K method by introducing first order strain gradient term in the constitutive equation. They found that, for the left hand side of the FLD, the stress ratios are constant throughout the deforming sheet including the homogeneous and non-homogeneous region if Hill's zero-extension direction is assumed along the direction of the initial imperfection. It is the first time that people have ever been able to quantitatively explain the difference in the FLDs from in-plane and out-of-plane deformation, a phenomenon observed by [Charpentier, 1975; Hecker, 1975].
1.3.2 The effect of material anisotropy and yield function
Sheet metals exhibit a highly anisotropic material behavior by cold rolling. It is therefore of major importance to extend the plastic instability analysis to anisotropic materials. Constitutive relations for the plastic yielding and deformation of anisotropic metals at a macroscopic level were proposed long ago by Hill in 1948 [Hill, 1950]. This theory was the simplest conceivable one for anisotropic materials, however, inevitable limitations of its range of validity have eventually become apparent. The original M-K analysis [Marciniak and Kuczynski 1965] was based on Hill's 1948 yield criterion [Hill 1950]. However, it can be seen from the comparison with experiments and predicted results [Painter and Pearce, 1974] that this analysis overestimates the limit strains towards the equibiaxial strain region, and underestimates the limit strains towards the plane strain region, particularly for materials with R values less than unity [such as aluminum or brass]. In addition, the calculated limit strains for the right hand side of the FLDs are very sensitive to the material anisotropy, a phenomenon which has not been observed in experiment. Sowerby and Duncan [1971] argued that the difference between these two stress states depends on the yield criterion and the shape of the corresponding yield locus. The effect of R on the FLDs depends on how the R-value affects the yield locus shape. Using Hill's 1948 [Hill, 1950] yield criterion, the stress ratios for positive strain ratios depend strongly on the value of R.
Later on, several non-quadratic anisotropic yield criteria have been proposed by several authors [Bassani, 1977; Goth, 1977; Hill, 1979; Hosford, 1985]. Most of these theories are limited by the assumption of planar isotropy. Only the one proposed by Goth can accommodate planar anisotropy of orthotropic sheet metal, but its usage is limited by the assumption of a fourth-order function.
Hill's 1979 yield criterion, taken with the assumption of the principle of equivalence of plastic work, was proposed to account for the so-called "anomalous behavior" of aluminum. This yield criterion has undergone application. One line of attack is represented by the work of Parmar and Mellor [1978]. They investigated the dependence of limit strains on the material anisotropy based on the M-K method and this non-quadratic yield function. However, they found that the conclusion about the effect of R is difficult to drawn when this criterion is used. Because as the anisotropy R is varied, different stress-exponents are required in order to produce yield loci with sensible shapes so that the effects of varying R are difficult to separate from those caused by varying the stress exponents. For this reason, when Hill published this yield criterion, he proposed four simple special cases from the general expression. Lian, et al. [1989] have thoroughly studied all the four cases and their limitations; they found that all the cases of the yield function except for one can provide reasonable predictions of the forming limits in the region of positive strain ratios.
In an effort to provide a new yield criterion with reduced dependence of the ratio of biaxial to uniaxial yield strength on the R value, Hosford [1985] developed an extension of Hill's 1948 yield criterion [Hill, 1950], which is also found to be a special case of Hill's 1979 yield criterion. This criterion has been used by Graf and Hosford [1989, 1990] for sheet metals with normal anisotropy. Later, Padwal and Chaturvedi [1992] also used Hosford's planar anisotropy yield criterion to analyze the instable behavior of strain localization. They found that the effect of planar anisotropy is negligible while the predictions are strongly dependent on exponent "a" [exponent in yield criterion]. Predictions with a=5,6 or 8 match the experimental results much better than the predictions that were obtained from Hill's yield criterion. They concluded that either an isotropic material may be assumed for the prediction of forming limits, or the value of average anisotropy R may be used. This anisotropic yield criterion suggested by Hosford reduces the overestimation of limit strains towards equibiaxial tension. The predictions are insensitive to planar anisotropy.
Even though Hill's 1979 and Hosford's yield criteria have been widely applied to predict forming limit diagrams, they have some limitations in application. They only consider the principal stress components, in other words, the loading are restricted to conditions in which the axes of principal stresses coincide with axis of material symmetry. Later Zhou [1990] improved Hosford's yield function by considering the shear stress components, so that it could be applied to general case.
Another non-quadratic anisotropic yield criterion proposed by Barlat and Lian [1989] includes a shear stress term in the expression of the effective stress, and this criterion makes it possible to predict FLDs for the complete range of strain ratios without the trouble which may occur by using Hill's 1979 or Hosford's nonquadratic yield criteria. This yield criterion has been used by Shi and Gerden [1991] and reasonable results have been obtained.
In 1982, an entirely different concept was adopted by Rasmussen [1982] to predict forming limit diagrams. He used a simple model of a material which develops a rounded vertex at the loading point, and studied the effect of rounded vertices on strain localization in sheets under balanced biaxial tension. This is also an extension of the M-K method. It was shown that the presence of rounded vertices drastically destabilizes plastic flow so that even very small imperfections in the sheet will lead to strain localization at realistic levels of deformation. Since the rounded vertex model inherently has a smooth yield surface, the imperfection sensitivity is such that limit strain tends to infinity as the imperfection tends to zero. Therefore Rasmussen's method would not predict localization in a perfect sheet at any reasonable level of deformation. However, he predicted a quite reasonable imperfection sensitivity when the strength imperfections of the sheet corresponded to thickness reductions of between 1% and 0.01%, which is considered to be representative for commercial sheets.
As to which yield criterion is better, Vial, et al. [1983] have conducted experiments with different combinations of R-values and strain-hardening behavior, and compared this experimental data with predictions based upon three different anisotropic yield criteria [Hill, 1950; Hill, 1979; Hosford, 1985]. They found that no single yield criterion proved to describe adequately all of the test results.
1.3.3 The effect of voids or damage
Conventional sheet materials generally contain second phase particles, introduced either as a by-product of the thermo-mechanical processing of the sheet, or intentionally in order to control microstructural features. During deformation, these second phase particles may debond from the surrounding matrix and crack, thereby nucleating voids which subsequently grow by plastic deformation. The important role played by this process of void nucleation and growth in ductile rupture has been recognized for a long time. This phenomenon limits the strains which can be achieved before the appearance of localized necking.
Assuming that a material containing voids deforms like a thinned region, Van Minh, et al. [1975] obtained the mean value and standard deviation of limit strains for forming a sample of sheet metal parts in a repeatable stretch forming process. They also assumed that tearing originates in defects in the material which can be characterized by an equivalent population of voids which have an exponential size distribution. They found that for a given material the mean limit strains will increase with material thickness, the severity of overall strain gradient and with decreasing volume fraction of equivalent voids. Numerical results indicated that the relationship between formability and volume fraction of voids is approximately of an inverse logarithmic nature.
An experiment was carried out by Parmar and Mellor [1980] to determine the void growth in sheet metals. They have shown that there are three stages in the density change of steel sheets stretched under balanced biaxial tension. In stage I, existing voids expand and new voids are initiated. Thus the void growth rate in this stage is the greatest. The value of in-thickness strain in this stage is below 0.2. In stage II, most of the voids have been initiated already and a constant number of voids expands. In this stage the void growth rate is lower than that of stage I. The value of thickness strain in this stage is between 0.2 and 0.4. In stage III, the deformation is concentrating in the region of the neck. Thus the overall density change rate in this stage is the lowest. The value of thickness strain in this stage is above 0.4 up to fracture.
Based on Gurson's yield criteria [Gurson, 1977] for porous ductile materials and the M-K method, Needleman and Triantafyllidis [1978] investigated the role of void growth in triggering localized necking in biaxially stretched sheets. They used an increased initial volume concentration of void within the incipient neck instead of a geometric imperfection. They found that the porous plastic material model predicted forming limit diagrams qualitatively in accord with experimental results. However, the results also show that any microstructural inhomogeneity that gives rise to a continually decreasing rate of hardening in the neck may be expected to predict qualitatively similar forming limit diagrams. They also found that the hypothesis of an equivalent thickness imperfection is not necessarily appropriate for high strength materials. Later, Kim and Kim [1983] assumed that a uniform void distribution at the beginning of stretching, and a thickness imperfection exists, then develops into a neck after the swift's instability condition [Swift, 1952] is attained. They found that the density change rate in stage III is lower than that of stage II, however, the local density change rate in the neck region in stage III is equal to the overall density change rate in stage II. Barata da Rocha [1989] also assumed that the material contains an initial internal damage due to the presence of voids. It is shown that the necking process strongly depends on this phenomenon.
Recently, Lee, et al [1985], Tai [1988], Chow, et al [1996] and Lee, et al [1997] have applied the concept of damage mechanics to anisotropic materials and have applied it to predict the forming limit diagrams for different materials.
1.3.4 The effect of texture or deformation dependent parameters
Most of the previous studies considered the initial anisotropy to be conserved during the forming operation. Only recently the role of the varying plastic anisotropy during biaxial deformation of sheet metals has been considered. Experimental data from Hu [1974, 1975] and Ghosh [1978] has shown that the material parameters, such as material anisotropy R and work-hardening exponent n, all change during deformation. Therefore, it is very important to study the effect of the variation of these parameters on the forming limit diagram.
Applying a rate-sensitive crystal plasticity model directly in connection with the M-K method, Zhou and Neale [1995] have been able to predict forming limit diagrams for annealed FCC sheet metals with various initial textures. They found that the localized neck occurs when the total accumulated shear over all slip systems in the band of localized deformation reaches a critical value, and the critical value depends only on the slip-induced hardening law. Different cyrstalline orientations result in different slip distributions for a specific deformation state; the slip distribution also affects the forming limit. On the other hand, different initial textures lead to different yield surface shapes before and during deformation, and this greatly affects the forming limit diagrams. The evolution of texture, and consequently of yield surface shape, during deformation may have a great influence on the forming limits. Wu, et al, [1998] confirmed this results in their investigation of the formability of aluminum.
Toth et al. [1996] examined the differences in the predicted limit strains which may be caused by the development of anisotropy during straining within the framework of the M-K theory. They found that both the initial textures and their subsequent development influence the limit strains.
1.3.5 The effect of strain path
Theoretical and experimental FLDs are usually determined for proportional strain paths. However, this hypothesis is no longer valid in the press shop since the strain paths are usually non-linear. Industrial stamping of complex shapes often involves multistage forming operations, and linear strain paths can no longer be obtained. The strain histories at different points of the workpiece is generally quite complex, and abrupt changes can take place.The forming limits are shown to be complex functions of strain histories. The effect of strain path on the forming limit diagrams has also been observed in experiments [Hecker, 1973; Kleemola and Pelkkikangas, 1977; Chu, 1983 and Graf and Hosford, 1994]
Modifying the M-K analysis, Lee and Kobayashi [1975] initiated a method for non-proportional deformation using a formulation in which the orientation of the incipient necking band is always perpendicular to the direction of major principal stress. This specific orientation of the band, however, leads to an overestimation of formability in those cases where the strain path includes negative strain increments. Rasmussen [1981] has given a formulation of MK analysis which allows for any strain path to be simulated and for the most critical orientation of necking bands to be determined. In this method, the forming limit is obtained for the groove orientation which leads to the minimum calculated limiting strain. He found that the initial band orientation was independent of the prestrain when the last deformation is biaxial stretching. However, for negative strain ratios the limiting strains are achieved with groove orientations dependent on the strain path. Later Rasmussen [1982] extended this method to analyze the effect of curvilinear strain paths.
Barata and co-workers [1984, 1985 and 1989] have studied the effect of strain path changes on the theoretical FLDs of isotropic rate-sensitive materials computed with MK method. It has been shown that uniaxial prestrain followed by balanced biaxial stretching considerably increases the limiting strains at the onset of necking. Conversely, premature instabilities were observed for strain paths consisting of prior balanced biaxial stretching followed by uniaxial tension. In addition, a change in strain path from balanced stretching towards plane strain deformation resulted in a significant loss of plastic stability. Kinematic hardening and rate sensitivity of flow stress have also been analyzed by Lu and Lee [1987] and Nie and Lee [1991]. Graf and Hosford [1994] determined the FLDs of aluminum alloy 6111 T4, and compared it with experimental data. Zhao et al. (1996] also considered the effect of strain path on the shape and magnitude of the FLD by considering material anisotropy, strain hardening and strain rate sensitivity.
From these analyses, it is found that prestrain in balanced biaxial tension generally lowers the entire FLD, whereas prestrain in uniaxial tension raises the limits on the right hand side of the FLD without much effect on the left hand side, when the direction of the largest principal strain does not change. If the directions of the principal strains are rotated, prestrain in uniaxial or plane strain tension lowers the forming limits for most of the FLD range. However, the remaining formability decreases with any kind of prestrain.
The above mentioned M-K method is a non-linear method, and thus computationally quite expensive. On the other hand, linear analysis can give explicit solutions for predicting limit strains, and it is easy to be applied to the actual press shop. Linear stability or bifurcation analysis has long been studied since the 1950's, and linear analytical methods has been able to give some useful results.
1.4.1 Swift's diffuse necking -
As early as in 1952, Swift [1952] developed a criterion for predicting the onset of diffuse necking with the assumption that plastic instability occurs at a load maximum for proportional loading. Swift has shown that the critical major strain for diffuse necking can be expressed as
where 
is the strain ratio (the minor strain over the major strain)
Swift's result can be thought of as a generalized condition, it can be applied to the whole range or deformation, i.e. from uniaxial tension to balanced-equibiaxial stretching. However, the onset of diffuse necking is not readily observable in a deformed sheet. Plastic instability leads to failure only when a localized neck forms, and the predicted limit strains are much lower than the experimental data when the strain ratio is negative. Therefore, the limit strains calculated from Swift's diffuse necking analysis are of limited practical interest.
1.4.2 Bifurcation method with flow theory
With the assumption that the onset of failure, or discontinuity of stress and velocity, leads to localized necking, Hill [1952] described the restrictions on the flow stress and rate of work hardening for the growth of localized necking. Hill explained how, during uniform deformation of a sheet, a localized sheet zone can develop along the zero-extension direction, which happens when the plastic work increment within the zone becomes less than that for uniform deformation. From Hill's analysis, the localized band angle, which is measured between the normal to the band and the major strain direction, is expressed by
From this result, it is seen that the angle have a real value only if the strain ratio is negative. Physically this means that when the strain ratio is positive, there is no angle at which a local neck can form and still fulfill the requirement of the existing of zero extension direction. In other words, the localized neck can not form under stretching conditions when the strain ratio is positive. However, localized necking can be observed experimentally in biaxially stretched sheets.
Using a power law stress-strain relation, 
, the critical condition for localized necking for negative strain ratio becomes
Later, Lee and Kobayashi [1975] and Korhonen [1978] used Swift's instability criterion when instability occurred with positive strain increment ratios, while Hill's criterion for localized necking was applied when the strain increment ratio was negative at instability. In these approaches, the influence of strain path on limiting strains are assumed that plastic instability depends on the prior deformation history through accumulated effective strain and on the instantaneous value of strain increment ratio. They obtained that a change towards equibiaxial tension generally increases the forming limits, a change towards plane strain having the opposite effect. The theoretical limit strains are influenced by the assumptions made concerning work-hardening and anisotropy. By using a similar method, Hillier [1966] and Negroni et al. [1968] studied the influence of strain path on sheet metal instability by assuming that instability occurs when the forces transmitted by the sheet reach a maximum. They also found that the instability is path dependent.
1.4.3 Bifurcations with vertex theory
The physical theory of plasticity, based on simple crystallographic slip models (Lin, 1971], predicts the development of a sharp vertex at the loading point on the yield surface of a polycrystalline aggregate. The concept of vertices or corners in the yield surface therefore is of major interest. The existence of such phenomena is supported by physical theories of plasticity and also by detailed experimental investigations [Hecker, 1976]. There is considerable evidence that the loading point carries with it a vertex part of the yield surface. Whether this is an actual sharp corner or a round vertex remains an unsolved problem, since it is impossible to differentiate experimentally between sharply rounded vertices and actual singular points in the yield surface.
Storen and Rice [1978] incorporated the J2 deformation theory of plasticity, which is a simplified model of the corner theory, into the classical bifurcation analysis to predict the localized necking over the entire range of the FLD. They postulated that localized necking is due to the development of a corner on the yield surface. Thus there is no theoretical restriction to localized necking. They found that the angle of the localized band is not in the zero extension direction when the strain ratio is negative, and the band always coincides with the minor strain direction for positive strain ratios. Because it is impossible to obtain the optimized band angle analytically, they have to use numerical method to calculate the limit strains for the left hand side of FLD. By assuming that the localized band coincides with the zero extension direction for the negative strain ratio, they were able to obtain an explicit expression for the critical strain, i.e.
Those formula can give reasonable limit strains for some strain rate insensitive materials when the strain ratio is positive, while they predict a too low forming limit when the strain ratio is negative. Accordingly, its application is limited.
Following a similar analytical framework, Hutchinson and Neale [1977c] predicted forming limits using both flow theory and deformation theory. Even though they have made some improvement, the forming limit for the left hand side is still not satisfactory. Since the assumption of proportional loading is inherent in these analyses, the predictions are carried out under the condition of simple proportional loading.
Chu [1982] took use of the result by Storen and Rice [1975], and extended it in order to predict the forming limit by considering the strain path. He assumed that the materials obey isotropic hardening rule, and he obtained that the stress state of the final step alone determines whether a local neck will be formed. Corresponding to this critical stress state there is an equivalent strain which limits the safe forming of sheet metals. This equivalent strain can be written in the form:
where 
denotes the limiting equivalent strain for sheets without prestrain, superscripts (i) represent the ith prestraining step.
An alternative approach is based on perturbation analysis. The sheet is assumed to be initially homogeneous. At any stage of the postulated homogeneous deformation process, a perturbation is superimposed on the basic homogeneous flow. It has been quite successfully developed in fluid mechanics and later it was used in solids mechanics for shear band analysis [Zbib, 1988], and for localized necking analysis in uniaxial tension [Fressengas and Molinari, 1985].
Dudzinski and Molinari [1991] first used the concept of effective instability, and then successfully adopted the instability method to prediction of forming limit diagrams. They found that the onset of instability appears to be of a little significance if the growth of the unstable modes is very slow. The effective instability analysis gives basically the same trends as the M-K method. The dependence of the limit strains on the value of the instability intensity parameter presents the same tendencies as the dependence of the limit strains on the amplitude of the initial defect in the M-K analysis. Later, Toth, Dudzinski and molinari [1996] improved the previous method by using viscoplastic crystallographic slips and Taylor approach. Considering plastic potentials and their development during large plastic deformation of textured aluminum sheets, the forming limit diagrams are obtained.
The instability method has many advantages over M-K method, most important is that an explicit expression for the critical strain can be obtained. However, it is found that the instability analysis can only obtain reasonable forming limit strains for some strain rate sensitive materials, while it predicts too low limit strains for steels, which is strain rate sensitive.
For finite deformations, the effect of material inhomogeneity becomes pronounced and has a dominant influence on the constitutive and instability behavior of polycrystalline solids. In order to account for this effect, a gradient theory of plasticity was developed by Aifantis (1984, 1987, 1992, 1994] and co-workers (e.g., Zbib and Aifantis, 1989, Muhlhaus and Aifantis, 1991] Vardoulakis and Aifantis, 1991] by introducing a gradient-dependent expression for the flow stress. A quite general expression for the flow stress is of the form
where (
) are the equivalent stress and strain, respectively, 
is the usual homogeneous part of the flow stress, and 
measures the heterogeneous or nonlocal character of the hardening mechanisms. Various forms of this function are possible, among them one of the simplest is
where the coefficients c1-c4 are all functions of 
. However, for simplicity, the c's are often chosen as constants which are independent of the deformation.
In the case of rate-independent materials the flow stress depends on the total deformation only and the flow stress reduces to
For a comprehensive understanding of the nature of the gradient coefficient. certain microscopically based arguments have already been advanced for its theoretical estimation. These estimations depend on the scale of interest and the particular deformation mechanisms involved [Muhlhaus and Aifantis, 1991, Vardoulakis and Aifantis, 1989, 1991].
The formability of most sheet metals is limited by the occurrence of a localized neck. This review examined attempts to theoretically predict forming limit diagram for sheet metals. From these studies, it is seen that the predicted forming limit diagrams are affected by many different factors, such as strain and strain rate sensitivity, the shape of the yield surface, the void volume fraction, most importantly, the strain path.
The M-K method has been widely used to predict forming limit diagrams, and the original M-K method has undergone tremendous improvement. With more and more realistic models, the predicted values can match the experimental data very well for most sheet metals. Up to today, the M-K method has become one of the most important tools in predicting the sheet metal formability. On the other hand, much less researches have been conducted by using the linear perturbation (or bifurcation) analysis, even though it can give an explicit expression of the critical strain.
Until now, all the above mentioned methods in predicting the forming limit diagrams are inconclusive. There are still lots of questions to be answered, for example, why the limit strains obtained from in-plane and out-of-plane deformation are so different? In addition, even though the M-K method has undergone significant improvement, it is still very difficult to apply this method to the actual press shop. This is because the fact that the M-K method is a non-linear method, it is difficult to solve the non-linear differential equation, further more, every improvement of this method means to make it more difficult. Accordingly, it is very important to have a method which can predict the forming limit diagram more realistically and be simple enough to be applied to the actual press shop.
